0. Abstract
- 대부분의 nlp 문제는 질문에 대한 대답(question answering) 문제로 간주될 수 있다.
- 여기서 소개하는 Dynamic Memory Network(DMN)은 input(정보)과 질문으로부터 episodic memory를 형성한다.
- 이를 이용하여 질문에 관련성이 높은 답변을 생성한다.
- 질문들은 반복적인 attention 과정을 통해서 input과 이전 시점의 결과에 대한 attention을 수행한다.
- 이 결과들은 hierarchical recurrent sequence model을 통해 질문에 대한 답변을 생성하는 데에 사용된다.
1. Introduction
- Question Answering은 텍스트의 의미 파악 및 관련된 정보에 집중할 수 있는 능력 모두가 요구되므로 어려운 NLP 과제이다.
- 대부분의(사실상 전부) NLP 과제들은 Question Answering으로 해석될 수 있다.
- 이 논문은 이 문제를 잘 해결할 수 있는 Dynamic Memory Network를 소개한다.
- 이는 input(정보)-question-answer로 구성된 데이터에 대하여 학습된다.
- 간략하게 DMN의 구조를 소개하자면,
- 모든 input들과 질문에 대한 대표값을 계산한다.
- 질문에 대한 대표값을 이용하여 input들로부터 관련된 정보를 얻기 위한 attention을 반복적으로 수행한다.
- memory module은 위 과정 이후, 관련도 높은 정보들을 통해 fact를 담고있는 벡터를 도출한다.
- fact 벡터를 이용하여 answer module은 적절한 답변을 생성한다.
- DMN이 학습한 데이터의 예시는 다음과 같다.
I: Jane went to the hallway.
I: Mary walked to the bathroom.
I: Sandra went to the garden.
I: Daniel went back to the garden.
I: Sandra took the milk there.
Q: Where is the milk?
A: garden
I: It started boring, but then it got interesting.
Q: What’s the sentiment?
A: positive
Q: POS tags?
A: PRP VBD JJ , CC RB PRP VBD JJ
2. Dynamic Memory Networks
- 이제 DMN을 구성하는 module들에 대하여 간단하게 알아보자.
- 아래와 같이 간단한 도식으로 표현할 수 있다.
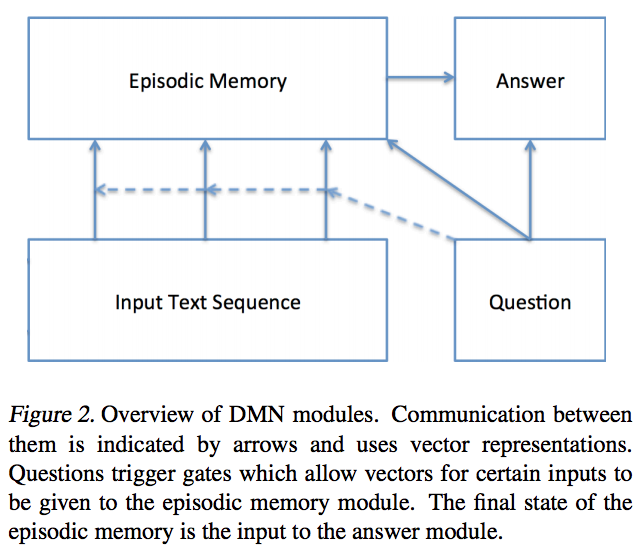
- 아래와 같이 간단한 도식으로 표현할 수 있다.
- Input Module
- 단일 문장, 줄글, 영화평, 뉴스기사, 위키피디아 글 등의 input을 벡터로 나타낸다.
- Question Module
- input 모듈과 마찬가지로 질문을 벡터로 나타낸다.
- 이 벡터는 episodic memory module의 initial state가 된다(iteration 0에서의 state).
- Episodic Memory Module
- attention mechanism을 이용하여, input 중 어디에 얼마나 집중해야하는지 계산한다.
- 이후, 이전의 memory와 질문을 종합적으로 고려하여, memory vector를 계산하는 과정을 반복한다.
- 이 과정에서 이전의 iteration에서는 찾지 못했던, input으로부터의 질문에 관련된 정보를 얻어낼 수 있다.
- Answer Module
- memory module의 마지막 memory vector를 이용하여 답변을 생성한다.
2.1 Input Module
- input은 \({ T }_{ I }\)개의 단어들의 sequence이다.
- \[w_{ 1 },...., w_{ { T }_{ I } }\]
- 여기서는 recurrent neural network의 hidden state를 이용하여 input sequence에 대한 embedding을 수행한다.
-
\[h_{ t }=RNN(L[w_{ t }],h_{ t-1 })\]
- L은 word embedding matrix
- \({w}_{t}\)는 해당 단어의 index
-
\[h_{ t }=RNN(L[w_{ t }],h_{ t-1 })\]
- input sequence가 단일 문장인 경우, input module은 각 단어에 해당되는 hidden state들을 output으로 반환한다.
- input module의 output은 단어의 개수만큼의 sequence이다(\({ T }_{ c }={ T }_{ I }\)).
- input sequence가 여러 문장들로 이루어진 경우, 각 문장 사이에 end token을 결합하여, 이를 하나의 단어들의 sequence로 간주한다.
- input module의 output은 각 end token에서 도출되는 hidden state들이다.
- 여러 문장 input의 경우, output은 문장의 개수만큼의 sequence이다.
- 최종적으로 도출되는 input module의 결과는 \({T}_{c}\) 개의 fact 대표값 sequence c이다.
- \({c}_{t}\)는 input module의 output sequence 중 t번째 값이다.
2.1.1 Choice of recurrent network
- 이 논문은 Gated Recurrent Network(GRU) 를 사용한다.
- 이는 vanishing gradient problem이 없어서 기본 RNN보다 나은 성능을 보였다.
- GRU의 수식적인 구성은 아래와 같다.
- r은 리셋 게이트로서, 새로운 입력을 이전 상태와 어떻게 합칠지 결정한다.
- z는 업데이트 게이트로서, 이전 상태를 얼마나 기억할지 결정한다.
- 리셋 게이트가 전부 1이고, 업데이트 게이트가 전부 0이면 기본적인 RNN 구조와 동일해진다.
- \(\circ\) 은 element-wise product이다
\[z_{ t }=\sigma ({ W }^{ (z) }x_{ t }+{ U }^{ (z) }h_{ t-1 }+b^{ (z) })\] \[r_{ t }=\sigma ({ W }^{ (r) }x_{ t }+{ U }^{ (r) }h_{ t-1 }+b^{ (r) })\] \[\tilde { h } _{ t }=tanh({ W }x_{ t }+r_{ t }\circ { U }h_{ t-1 }+b^{ (h) })\] \[h_{ t }=z_{ t }\circ h_{ t-1 }+(1-z_{ t })\circ \tilde { h } _{ t }\]
- \(\circ\) 은 element-wise product이다
2.2 Question Module
- input module과 동일하게, GRU를 이용하여 질문을 embedding한다.
- 차이점은, question의 경우, 가장 마지막 hidden state 하나만을 output으로 출력한다는 것이다.
- 즉, \(q_{ t }=GRU(L[{ w }_{ t }^{ Q }],q_{ t-1 })\) 이며, 최종 출력 \(q={ q }_{ { T }_{ Q } }\) 이다.
- 여기서 word embedding matrix는 모두 동일하게 사용된다.
2.3 Episodic Memory Module
- input module의 아웃풋에 대해 iterate 하며, 내부의 episodic memory를 업데이트 한다.
- 업데이트는 attention mechanism과 rnn을 이용한다.
- 간략한 과정은 아래와 같다.
- fact 대표값 c, 질문 대표값 q, 이전의 memory \({m}^{i-1}\) 를 이용하여 episode \({e}^{i}\) 를 생성한다.
- 이전 memory \({m}^{i-1}\) 와 현재의 episode \({e}^{i}\) 를 이용하여 episodic memory \({m}^{i}\) 를 생성한다.
- \[{m}^{i}=GRU({e}^{i},{m}^{i-1})\]
- 최초의 GRU의 state는 question vector 그 자체이다(\({m}^{0}=q\)).
- 쉽게 생각해서 관련 정보를 하나씩 이어나가는데, 그 첫 연결고리는 질문 그 자체이다.
- \({T}_{M}\) 만큼 위 과정을 수행한 뒤, \({ m }^{ { T }_{ M } }\)이 answer module로 들어간다.
2.3.1 Need for Multiple Episodes
- 메모리 모듈은 iterative하게 실행되므로, 매 기마다 다른 input에 집중할 수 있다.
- 이 때문에, 하나의 fact에서만 얻을 수 없는 정보들은 얻어낼 수 있다.
- 어떠한 순서적인 정보(?)를 캐치해낼 수 있다.
- 아래 예시를 통해 확인하면 쉽다.
- 처음에는 단순히 football이라는 단어가 위치한 7번째 fact에 집중했다.
- 해당 문장에서 John이 존재한다는 사실을 파악하여 다음 시도에서는 John이 포함된 문장에 집중하게 된다.
- 이는 반복적인 attention의 장점이다.
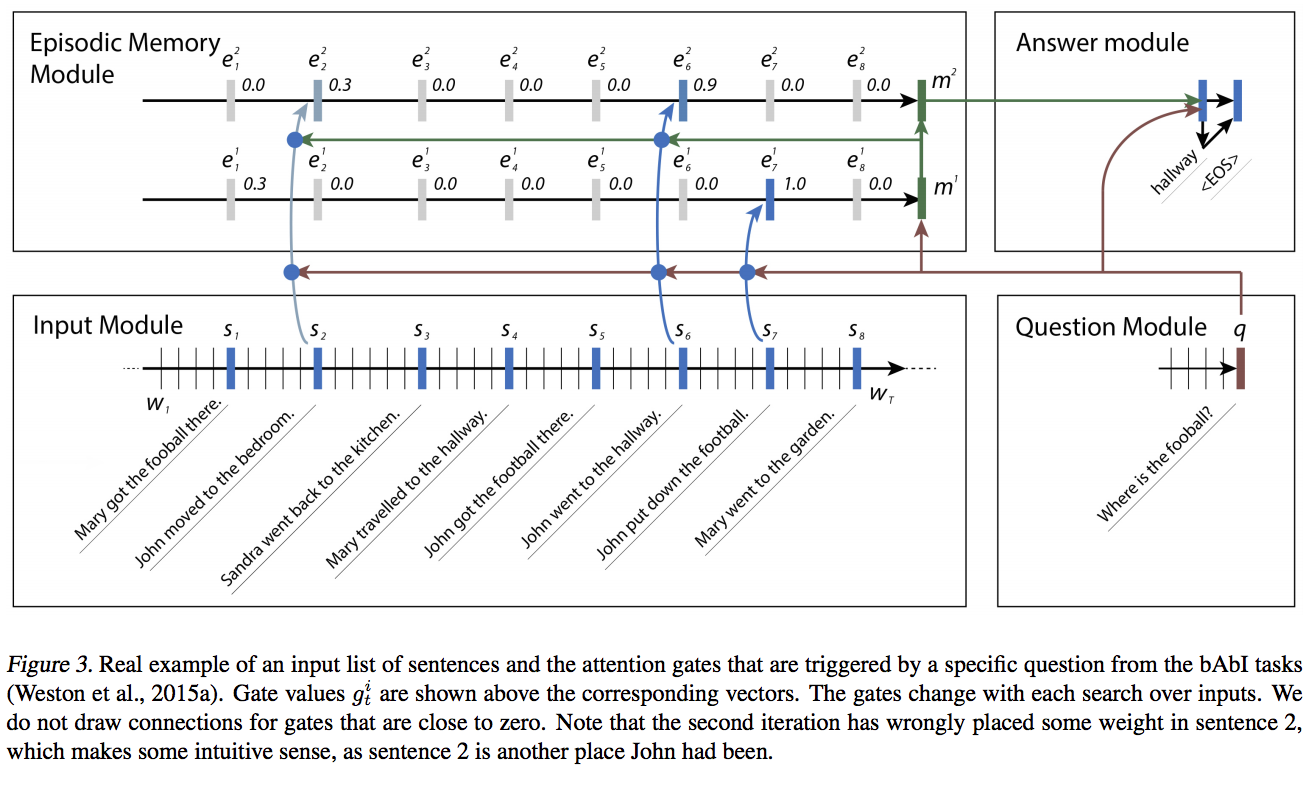
2.3.2 Attention Mechanism
- attention mechanism으로 gating function을 사용하였다.
- 매 pass(시행) i 마다, 이 구조체(?)는 후보 fact \({c}_{t}\), 이전 memory \({m}^{i-1}\), 질문 q를 받아 아래의 연산을 통해 gate를 구한다.
- \[{ g }_{ t }^{ i }=G(c_{ t },m^{ i-1 },q)\]
- scoring function G는 input으로 feature set z(c,m,q)를 받아서 scalar score를 계산한다.
- 여기서 z(c,m,q)는 input, memory, question 벡터들의 다양한 유사성을 담고있는 벡터이다. 아래와 같이 구한다.
- \[z(c,m,q)=[c,m,q,c\circ q,c\circ m,\left| c-q \right| ,\left| c-m \right| ,{ c }^{ T }{ W }^{ (b) }q,{ c }^{ T }{ W }^{ (b) }m]\]
- G는 단순 two-layer feed forward NN이다.
- \[G(c,m,q)=\sigma ({ W }^{ (2) }tanh({ W }^{ (1) }z(c,m,q)+b^{ (1) })+b^{ (2) })\]
- Facebook’s bAbI 데이터처럼 무엇이 질문에 대한 중요한 정보인가가 표시되어있는 경우, supervised learning이 가능하다.
2.3.3 Memory Update Mechanism
- i번째 pass의 episode를 계산하기 위해 \({c}_{1},...,{c}_{t}\)의 fact에 대해 수정된 GRU를 적용한다.
- gates \({g}^{i}\) 만큼 가중치를 곱한다.
- answer module에는 마지막 GRU state가 들어간다.
- t기의 GRU의 state와, episode를 계산하는 식은 아래와 같다.
- \[{ h }_{ t }^{ i }={ g }_{ t }^{ i }GRU(c_{ t },{ h }_{ t }^{ i-1 })+(1-{ g }_{ t }^{ i }){ h }_{ t }^{ i-1 }\]
- \[e^{ i }={ h }_{ { T }_{ c } }^{ i }\]
- 헷갈릴 것 같아서 명시합니다.
- i는 pass이며, 몇 번째 iteration인지를 의미합니다.
- t는 time이며, 몇 번째 fact인지를 의미합니다.
2.3.4 Criteria for Stopping
- iteration 을 멈추기 위하여, input으로 iterateion을 멈추는 token을 하나 더 추가한다.
- 이 input이 gate function에 의하여 선택되면 iteration을 멈춘다.
- supervised learning이 불가한 경우, max iteration을 정해놓는다.
2.4 Answer Module
- 마지막에 한 번만 발현되거나, episodic memory의 매 time step마다 발현되거나.
- 새로운 GRU를 또 적용한다.
- initial state : last memory \(a_{ 0 }=m^{ { T }_{ M } }\)
- 매 timestep 마다 질문 q, 지난 hidden step \({a}_{t-1}\), 이전 step의 output \({y}_{t-1}\) 을 받는다.
- \[y_{ t }=softmax({ W }^{ (a) }a_{ t })\]
- \[a_{ t }=GRU([y_{ t-1 },q],a_{ t-1 })\]
- 최종 아웃풋은 cross entropy로 학습.